Definición
En lógica proposicional y álgebra Booleana,
las leyes de De Morgan son un par de reglas de transformación que
son ambas reglas de inferencia válidas. Las normas permiten la expresión de las conjunciones y disyunciones puramente
en términos de vía negación.
Las reglas se pueden expresar en español como:
La negación de la conjunción es la disyunción de las
negaciones.
La negación de la disyunción es la conjunción de las negaciones.
La negación de la disyunción es la conjunción de las negaciones.
o informalmente como:
"no (A y B)" es lo mismo que "(no
A) o (no B)"
y también,
"no (A o B)" es lo mismo que "(no
A) y (no B)"
Las reglas pueden ser
expresadas en lenguaje formal con
dos proposiciones P y Q, de esta forma:
donde:
- es el operador de negación (NO)
- es el operador de conjunción (Y)
- es el operador de disyunción (O)
- es un símbolo metalógico que significa "puede ser reemplazado
en una prueba lógica"
Entre las aplicaciones de
las normas se incluyen la simplificación de expresiones lógicas
en programas de computación y
diseño de circuitos digitales. Las leyes de De Morgan son un ejemplo de
concepto más general de dualidad matemática.
Suma de Productos y Producto de Sumas
Cuando se trabaja con expresiones booleanas, es
deseable que estas se encuentren expresadas en una de dos formas: como suma de
productos o como producto de sumas.
Una suma de productos consiste de dos o más grupos
de literales, cada literal es recibida como entrada por un AND y la salida de
cada una de estas compuertas (AND) es recibida como entrada por una compuerta
OR.
es decir, el circuito combinatorio de una suma
de productos debe de tener el siguiente patrón:
Un producto de sumas consiste de dos o más
grupos de literales, cada literal es recibida como entrada por un OR y la
salida de cada una de estas compuertas (OR)es recibida como entrada por una
compuerta AND.
es decir, el circuito combinatorio de un
producto de sumas debe de tener el siguiente patrón:
Se puede pasar una expresión booleana a suma
de productos o producto de sumas utilizando las leyes distributivas vistas
anteriormente.
Ejemplo.
Ejemplo.
Finalmente, los siguientes teoremas permiten
convertir a producto de sumas o suma de productos una expresión de manera
sencilla:
Ejemplo. Convertir a suma de productos:
Ejemplo. Convertir a producto de sumas:
Para mayor comprensión del tema, visualiza el siguiente video desde la plataforma de youtube:https://www.youtube.com/watch?v=6fXE2_67z_Q
















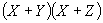









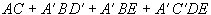

No hay comentarios.:
Publicar un comentario