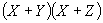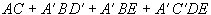Hola a todos me llamo
Ileana Andreina Balboza Colina Ci:27-508-487 soy estudiante de la Escuela 47
Ingeniería De Sistemas, me encuentro cursando la materia de Electronica Digital
en la seccion "SA", Con el fin de adquirir conocimientos sobre dicha
materia y asi reforzar lo que hasta ahora he aprendido sobre esta maravillosa
carrera.
Electrónica Digital
Sección "SA"
martes, 21 de enero de 2020
Algebra Booleana
Definición.
El álgebra booleana es un sistema matemático deductivo
centrado en los valores cero y uno (falso y verdadero). Un operador binario
" º " definido en éste juego de valores acepta un par de entradas y
produce un solo valor booleano, por ejemplo, el operador booleano AND acepta
dos entradas booleanas y produce una sola salida booleana.
Para cualquier sistema algebraico existen una serie de
postulados iniciales, de aquí se pueden deducir reglas adicionales, teoremas y
otras propiedades del sistema, el álgebra booleana a menudo emplea los
siguientes postulados:
Cerrado. El sistema booleano se considera cerrado con
respecto a un operador binario si para cada par de valores booleanos se produce
un solo resultado booleano.
Conmutativo. Se dice que un operador binario " º
" es conmutativo si A º B = B º A para todos los posibles valores de A y
B.
Asociativo. Se dice que un operador binario " º "
es asociativo si (A º B) º C = A º (B º C) para todos los valores booleanos A,
B, y C.
Distributivo. Dos operadores binarios " º " y
" % " son distributivos si A º (B % C) = (A º B) % (A º C) para todos
los valores booleanos A, B, y C.
Identidad. Un valor booleano I se dice que es un elemento
de identidad con respecto a un operador binario " º " si A º I = A.
Inverso. Un valor booleano I es un elemento inverso con
respecto a un operador booleano " º " si A º I = B, y B es diferente
de A, es decir, B es el valor opuesto de A.
Para nuestros propósitos basaremos el álgebra booleana en
el siguiente juego de operadores y valores:
- Los dos posibles valores en el sistema booleano son cero
y uno, a menudo llamaremos a éstos valores respectivamente como falso y
verdadero.
- El símbolo ·
representa la operación lógica AND. Cuando se utilicen nombres de
variables de una sola letra se eliminará el símbolo ·, por lo tanto AB representa la operación
lógica AND entre las variables A y B, a esto también le llamamos el producto
entre A y B.
- El símbolo "+" representa la operación lógica
OR, decimos que A+B es la operación lógica OR entre A y B, también llamada la
suma de A y B.
- El complemento lógico, negación ó NOT es un operador
unitario, en éste texto utilizaremos el símbolo " ' " para denotar la
negación lógica, por ejemplo, A' denota la operación lógica NOT de A.
- Si varios operadores diferentes aparecen en una sola
expresión booleana, el resultado de la expresión depende de la procedencia de
los operadores, la cual es de mayor a menor, paréntesis, operador lógico NOT,
operador lógico AND y operador lógico OR. Tanto el operador lógico AND como el
OR son asociativos por la izquierda. Si dos operadores con la misma procedencia
están adyacentes, entonces se evalúan de izquierda a derecha. El operador
lógico NOT es asociativo por la derecha.
Utilizaremos además los siguientes postulados:
P1 El álgebra booleana es cerrada bajo las operaciones AND,
OR y NOT
P2 El elemento de identidad con respecto a · es uno y con respecto a + es cero. No existe elemento de identidad para
el operador NOT
P3 Los operadores ·
y + son conmutativos.
P4 · y + son
distributivos uno con respecto al otro, esto es, A· (B+C) = (A·B)+(A·C) y A+
(B·C) = (A+B) ·(A+C).
P5 Para cada valor A existe un valor A' tal que A·A' = 0 y
A+A' = 1. Éste valor es el complemento lógico de A.
P6 · y + son ambos
asociativos, ésto es, (AB) C = A (BC) y (A+B)+C = A+ (B+C).
Es posible probar todos los teoremas del álgebra booleana
utilizando éstos postulados, además es buena idea familiarizarse con algunos de
los teoremas más importantes de los cuales podemos mencionar los siguientes:
Teorema 1: A + A = A
Teorema 2: A · A = A
Teorema 3: A + 0 = A
Teorema 4: A · 1 = A
Teorema 5: A · 0 = 0
Teorema 6: A + 1 = 1
Teorema 7: (A + B)' = A' · B'
Teorema 8: (A · B)' = A' + B'
Teorema 9: A + A · B = A
Teorema 10: A · (A + B) = A
Teorema 11: A + A'B = A + B
Teorema 12: A' · (A + B') = A'B'
Teorema 13: AB + AB' = A
Teorema 14: (A' + B') · (A' + B) = A'
Teorema 15: A + A' = 1
Teorema 16: A · A' = 0
Los teoremas siete y ocho son conocidos como Teoremas de De
Morgan en honor al matemático que los descubrió.
Ley conmutativa :
el orden de aplicación de dos términos separados no es importante
Ley
asociativa : esta ley permite
eliminar corchetes de una expresión y reagrupar las variables.
Ley
distributiva : esta ley
permite la multiplicación o factorización de una expresión.
Leyes del Álgebra Booleana Ejemplo
Usando las leyes anteriores, simplifique la siguiente expresión: (A + B) (A + C)
Luego, la
expresión: (A + B) (A + C) se puede simplificar a A + (BC) como en la ley
distributiva
Tablas
de la verdad para las leyes de Boolean
Para mayor comprensión del tema, visualiza el siguiente video desde la plataforma de youtube: https://www.youtube.com/watch?v=p58C7OWe3Xk
Ley de Morgan
Definición
En lógica proposicional y álgebra Booleana,
las leyes de De Morgan son un par de reglas de transformación que
son ambas reglas de inferencia válidas. Las normas permiten la expresión de las conjunciones y disyunciones puramente
en términos de vía negación.
Las reglas se pueden expresar en español como:
La negación de la conjunción es la disyunción de las
negaciones.
La negación de la disyunción es la conjunción de las negaciones.
La negación de la disyunción es la conjunción de las negaciones.
o informalmente como:
"no (A y B)" es lo mismo que "(no
A) o (no B)"
y también,
"no (A o B)" es lo mismo que "(no
A) y (no B)"
Las reglas pueden ser
expresadas en lenguaje formal con
dos proposiciones P y Q, de esta forma:{\displaystyle
\neg (P\land Q)\iff (\neg P)\lor (\neg Q)}
{\displaystyle \neg (P\lor Q)\iff
(\neg P)\land (\neg Q)}donde:
- es el operador de negación (NO)
- {\displaystyle \land } es el operador de conjunción (Y)
- {\displaystyle \lor } es el operador de disyunción (O)
- es un símbolo metalógico que significa "puede ser reemplazado
en una prueba lógica"
Entre las aplicaciones de
las normas se incluyen la simplificación de expresiones lógicas
en programas de computación y
diseño de circuitos digitales. Las leyes de De Morgan son un ejemplo de
concepto más general de dualidad matemática.
Suma de Productos y Producto de Sumas
Cuando se trabaja con expresiones booleanas, es
deseable que estas se encuentren expresadas en una de dos formas: como suma de
productos o como producto de sumas.
Una suma de productos consiste de dos o más grupos
de literales, cada literal es recibida como entrada por un AND y la salida de
cada una de estas compuertas (AND) es recibida como entrada por una compuerta
OR.
es decir, el circuito combinatorio de una suma
de productos debe de tener el siguiente patrón:
Un producto de sumas consiste de dos o más
grupos de literales, cada literal es recibida como entrada por un OR y la
salida de cada una de estas compuertas (OR)es recibida como entrada por una
compuerta AND.
es decir, el circuito combinatorio de un
producto de sumas debe de tener el siguiente patrón:
Se puede pasar una expresión booleana a suma
de productos o producto de sumas utilizando las leyes distributivas vistas
anteriormente.
Ejemplo.
Ejemplo.
Finalmente, los siguientes teoremas permiten
convertir a producto de sumas o suma de productos una expresión de manera
sencilla:
Ejemplo. Convertir a suma de productos:
Ejemplo. Convertir a producto de sumas:
Para mayor comprensión del tema, visualiza el siguiente video desde la plataforma de youtube:https://www.youtube.com/watch?v=6fXE2_67z_Q
Mapa de Karnaugh
Mapa de karnaugh
Definición
Un mapa de Karnaugh
(también conocido como tabla de Karnaugh o diagrama de Veitch, abreviado como
Mapa-K o Mapa-KV) es un diagrama utilizado para la simplificación de funciones
algebraicas Booleanas. El mapa de Karnaugh fue inventado en 1953 por Maurice
Karnaugh, un físico y matemático de los laboratorios Bell.
Los mapas de Karnaugh
reducen la necesidad de hacer cálculos extensos para la simplificación de
expresiones booleanas, aprovechando la capacidad del cerebro humano para el
reconocimiento de patrones y otras formas de expresión analítica, permitiendo
así identificar y eliminar condiciones muy inmensas.
El mapa de Karnaugh
consiste en una representación bidimensional de la tabla de verdad de la
función a simplificar. Puesto que la tabla de verdad de una función de N
variables posee 2N filas, el mapa K correspondiente debe poseer también 2N
cuadrados. Las variables de la expresión son ordenadas en función de su peso y
siguiendo el código Gray, de manera que sólo una de las variables varía entre
celdas adyacentes. La transferencia de los términos de la tabla de verdad al
mapa de Karnaugh se realiza de forma directa, albergando un 0 ó un 1,
dependiendo del valor que toma la función en cada fila. Las tablas de Karnaugh
se pueden fácilmente realizar a mano con funciones de hasta 6 variables, para
funciones de mayor cantidad de variables es más eficiente el uso de software
especializado.
Simbología
Un término irrelevante en
una expresión booleana es el resultado de la combinación de valores lógicos de
variables no requeridas para la solución de un problema específico. Estos
términos se simbolizan en el mapa en vez de 0 ó de 1 por “x”. Dichos símbolos
pueden utilizarse para conformar adyacencias con las cuales se ayuda a realizar
simplificaciones importantes. En el argot de la electrónica estos términos
producen condiciones que se denominan “don’t care” o “no
importa”.
Ejemplo 13.12: Dado el siguiente mapa
(Tabla 13.17) con términos irrelevantes marcados con “x”, obtenga la expresión
simplificada resultante
La expresión correspondiente
La expresión correspondiente



Para mayor comprensión del tema, visualiza el siguiente video desde la plataforma de youtube:https://www.youtube.com/watch?v=8WgEmX0ExaY
Suscribirse a:
Comentarios (Atom)